지난 포스팅에서 파이썬을 이용해 타원을 만드는 코드를 알아보았 습니다.
파이썬을 이용하여 타원 방정식 그래프 그리기
지난 포스팅에서 타원 방정식을 이용해 위도별 지구 반지름을 계산해 보았습니다. 그리고 가만히 생각해 보니, 행성들도 모두 타원, 별이나 행성들의 공전궤도면도 거의 대부분 타원 입니다. 그
kalchi09.tistory.com
사실 타원이라는것이 천체의 공전궤도, 행성의 모양 등 지구과학 전반에서 매우 많이 다루는데, 안타깝게도 학생들은 예전처럼 수학을 다 배우는게 아니고 기하라는 과목을 선택한 아이들만 타원이 뭔지를 알고 있는 그런상황입니다. 그러다보니 원이나 타원이 무엇인지 정확하게 모른채로 수업을 해야 해서, 수학시간도 아닌데 타원의 정의를 먼저 수업해 버리는 경우가 많습니다.
그래서 여기서는 행성들이나 별들 대부분의 공전 궤도이기도 한 타원이 무엇인지 정확히 알아보고자 합니다.
1. 원의 수학적 정의
원은 수학에서 이렇게 정의합니다
어느 한 점을 기준으로 거리가 같은 곳에 있는 평면위의 점들을 모두 이은 것
예를 들어 한 점을 원점 (0,0)이라고 하고, 여기서부터 거리가 3cm로 모두 같은 곳을 점을 찍으면 됩니다. 쉽게 생각하면, 길다란 종이의 양 끝에 작은 구멍 두 개를 뚫고 한쪽에 볼펜을 꼽고 이 볼펜을 고정, 다른 한쪽 구멍에 볼펜을 꼽고 삥 돌리면 두 구멍의 거리는 변하지 않으니 원이 쭉 그려집니다. (요게 참고로 콤파스 없을 때 원 그리는 꿀팁.ㅎㅎㅎ) 어쨌든 한 점에서 거리가 같은 모든 곳이니 아래 그림과 같이 완벽한 원이 나옵니다.

2. 타원의 수학적 정의
타원은 그냥 찌그러진 원?ㅋㅋ 이렇게 정의하면 안됩니다^^;; 원은 한 점에서 거리가 같은 곳을 점으로 찍고 그걸 연결한 것이다 라고 정의한다면, 타원은 두 개 점이 필요합니다. 두 점으로부터의 거리의 합이 일정한 곳을 선으로 연결한 것이 타원입니다. 그래서 원 처럼 중심이 중요하다기 보다, 위에 정의에서 언급한 두 점이 더 중요합니다. 요 두 점을 초점이라고 합니다. 타원을 작도하는 방법은 굉장히 쉽고 재미있습니다. 길다란 실 하나를 준비하고, 실의 양쪽 끝 부분을 압정같은걸로 고정합니다. 그리고 실 중간에 펜을 걸고 최대한 팽팽하게 한 뒤 쭉 둘러치면 타원이 쉭 그려집니다(이건 영상을 찍어서 올릴 예정입니다.)

위 그림은 제가 장반경이 15, 단방경이 10인 타원을 그린 것입니다. 이렇게 되면 두 초점 중 하나는 -11.2, 다른 하나는 11.2가 되는 타원이 그려집니다. 앞서 이야기 한 것 처럼 두 초점에서부터 거리의 합은 언제나 같아 집니다.
3. 타원의 구성
타원은 원과는 달리 알아둘게 꾀나 많습니다.. 그래서 여기서부터는 타원의 구성에 대해 알아보겠습니다. 우선 장반경과 단반경인데, 장반경은 타원의 중심에서 선이 가장 긴 놈, 보통 a로 표기하고, 단반경은 타원의 중심에서 선이 가장 짧은 놈, 보통 b로 표기합니다. 아래 그림을 참고하세요.

다음으로 이심율을 알아보겠습니다.

r1과 r2가 위 그림과 같이 되도록 만들면, r1+r2=2a, 그러니까 두 초점의 합은 결국 장반경의 2배가 됩니다. 만약 r1+r2=2a를 아래 그림과 같이 놓으면,
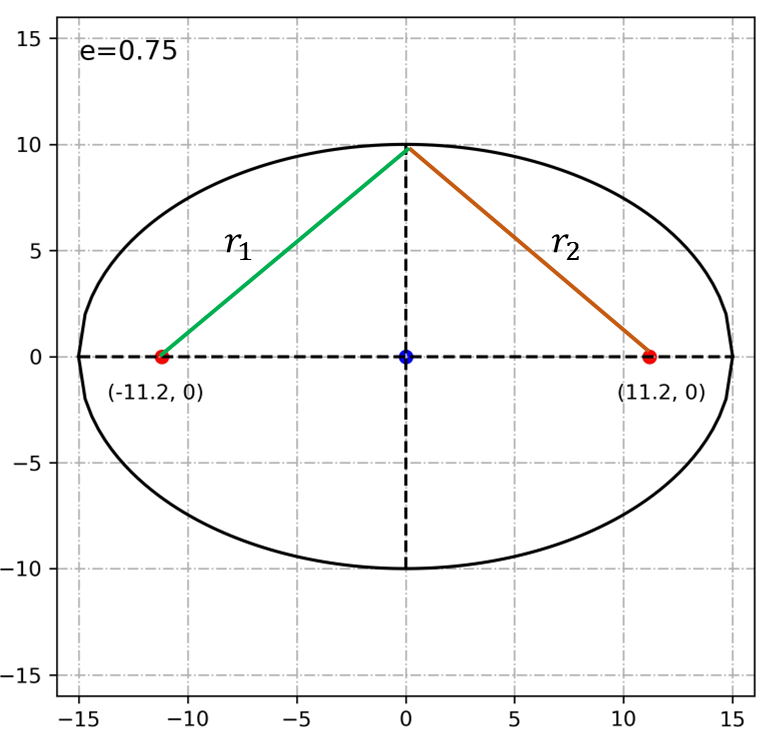
이 경우, r1의 길이와 r2의 길이가 완전히 같아집니다. 그래서 r1+r2를 r2+r2 이런 식으로 써도 됩니다. 그러면 r2+r2=2a 다시말해, 저 상황에서 r1과 r2의 길이는 그냥 장반경 a가 됩니다. 그리고, 초점에서 부터 타원의 중심까지의 거리를 c로 정의하면, 아래 그림처럼 됩니다.
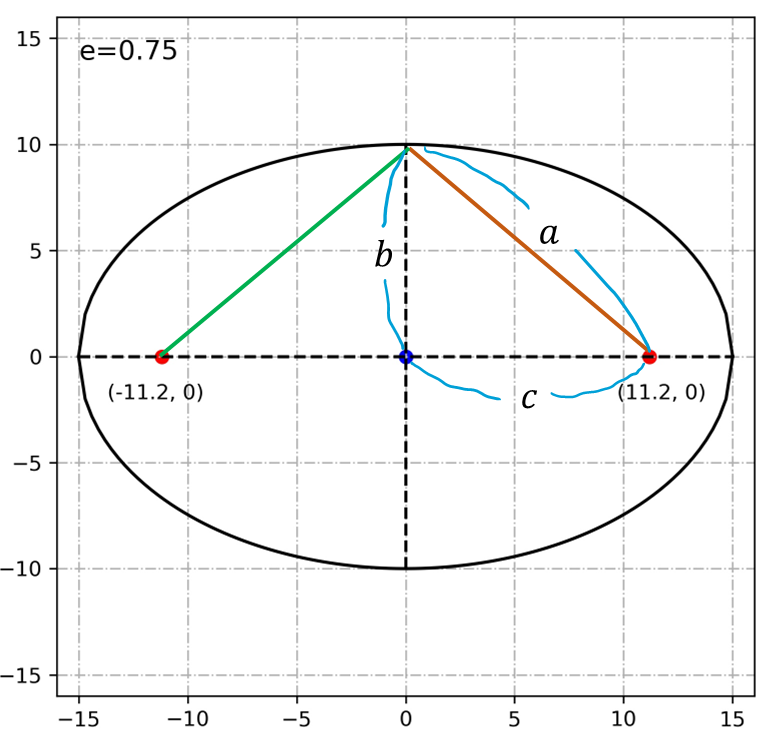
이제 장반경 a와 단반경 b, 그리고 초점까지의 거리 c의 관계를 간단히 정리할 수 있습니다.
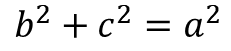
타원에서 이심률, 다시말해 원이 찌그러진 정도는 장반경과 초점까지 거리의 비로 정의합니다. 많이 찌그러진 타원일 수록 두 초점이 중심에서 멀리 떨어져 있고, 원에 가까운 타원일 수록 두 초점이 중심에 가까이 있습니다.
따라서 이심률은
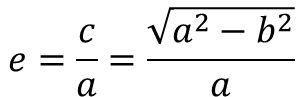
로 정의할 수 있습니다.
그래서 지난번 포스팅때 보았던 아래와 같은 짤이 나옵니다.
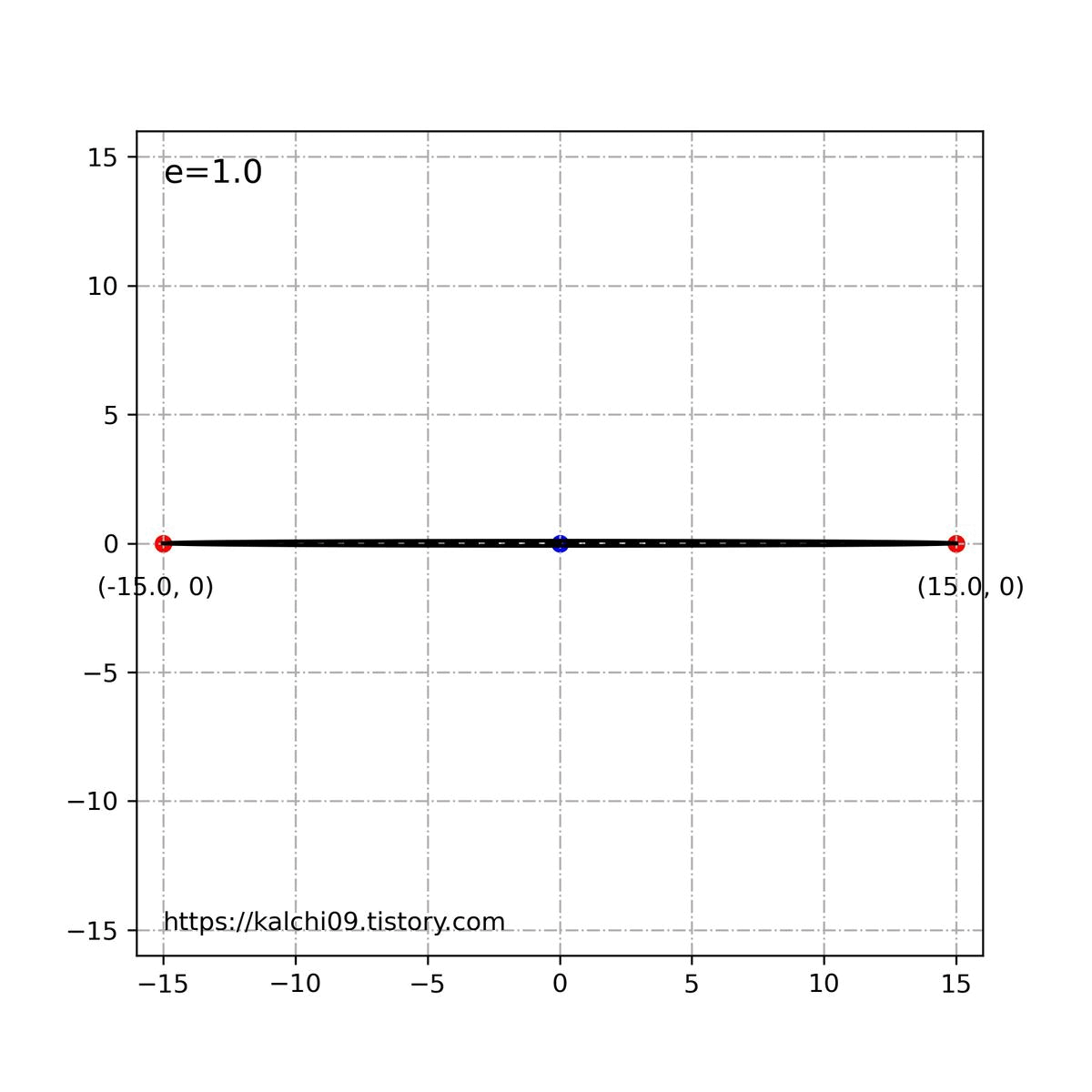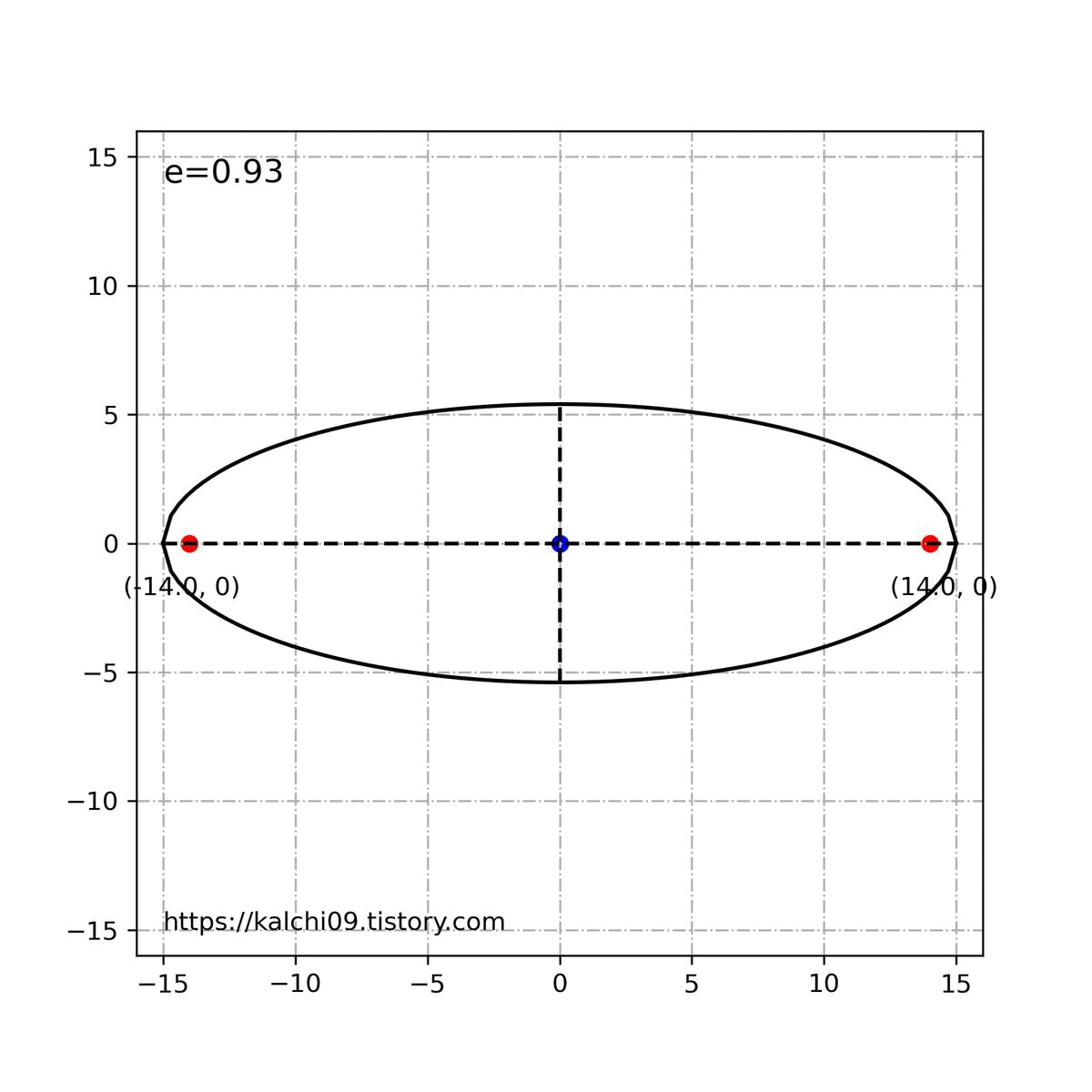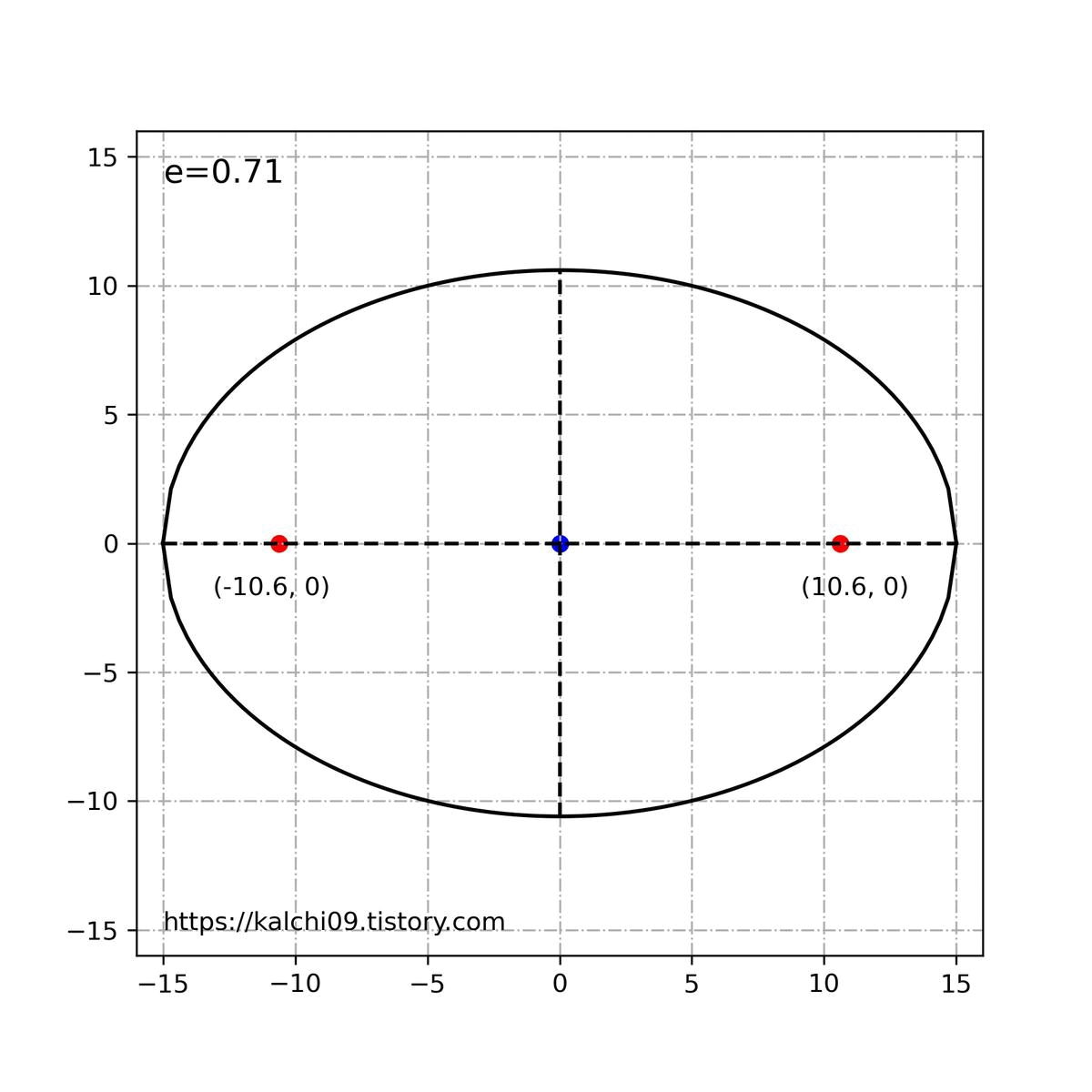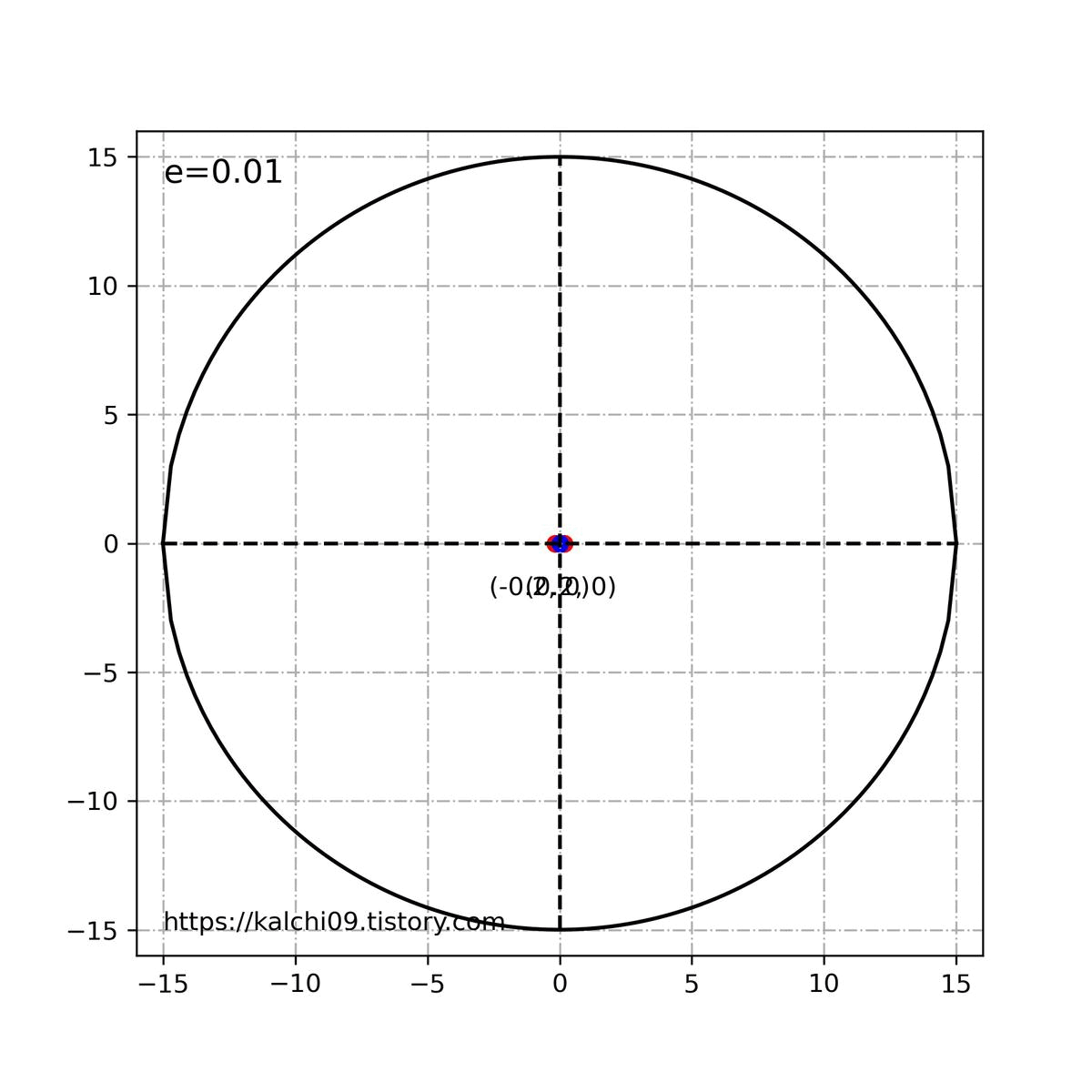
위의 내용을 바탕으로 타원의 이심률은 0<e<1 의 값을 가지게 됩니다. 원은 e=0이 됩니다. 쌍곡선과 포물선의 경우는 본 주제를 넘어서기 때문에 따로 언급하지는 않겠습니다.
4. 타원의 수학적 표현
사실 지구과학2나 지구과학1 수준에서 타원을 수학적으로 표현하는건 그리 중요한 내용은 아닙니다. 하지만 천문학에서 타원을 수학으로 표현하는건 한 번쯤은 해 볼 필요가 있습니다. 그래서 함께 알아보겠습니다(만, 이건 인터넷의 다른글을 찾아보아도 얼마든지 있긴 합니다)
수학에서 원은 기본적으로 아래와 같이 표현됩니다.
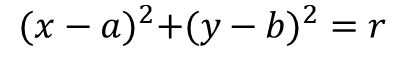
여기서 a와 b는 각각 원의 중심 좌표가 되고, r은 원의 반지름이 됩니다. 타원도 이거랑 비슷합니다.
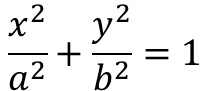
중심이 알파, 베타만큼 이동한 경우는 아래와 같습니다.
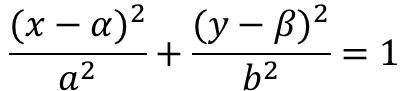
삼각함수 형식으로도 표현할 수 있습니다.

다음번에는 더 유익하고 재미있는 글을 준비하겠습니다.
그나저나 요즘 너무 바빠서 글 쓸 시간이 없네요..ㅠㅠ
'교과서 밖 지구과학 > 천문' 카테고리의 다른 글
| 별자리로 배우는 천문학 - 오리온 자리 (0) | 2023.04.24 |
|---|---|
| 지구과학에서 매우 중요한 도플러 효과에 대한 이해 (1) | 2022.07.23 |
| 별의 시선속도와 접선속도, 그리고 공간속도 (2) | 2022.07.04 |
| 태양계의 떠돌이 별 혜성 (0) | 2022.06.13 |
| 신비한 오로라 현상 (0) | 2022.06.03 |




댓글