하늘의 별은 그 어떤것도 가만히 있지 않습니다. 우리가 육안으로 볼 수 있는 우리 은하에 있는 구성별들은 거의 모두 모조리 은하 중심을 공전하고 있다고 생각해도 됩니다. 다만, 우리 태양도 공전하고 있기에 정지해 있는 것 처럼 보일 때도, 움직이는 것 처럼 보일때도 있는 것입니다. 오늘 다룰 내용은 이런 별의 시선속도, 접선속도, 공간속도에 대한 기본적인 내용들을 다루어 보고자 합니다.

1. 개요
별의 운동은 공간상에서 나타납니다. 다만 우리는 천구에 투영된 모습만 볼 수 있고, 거리의 변화는 느끼지 못합니다. 따라서 천구상에서 육안으로 식별 가능한 움직임은 천구면에 접한 부분 뿐 입니다. 그래서 별이 실제로 움직이는 운동 성분을 천구면에 접한 성분인 접선속도와 시선방향의 성분인 시선속도로 벡터 분해를 하여 표현합니다.

위 그림은 이 내용을 풀어 설명해 보고자 제가 그린 그림이라 다소 거북스럽지만(ㅠㅠ) 내용을 이해하는데 큰 어려움은 없을 것입니다. 관측 가능한 별들은 대부분 너무나도 멀리 있기 때문에, 거리를 인지할 수 없고, 단순한 육안관측만으로 멀어지고 가까워지는 것을 알 수 없습니다. 이렇게 우리 시선 방향의 속도 성분을 시선 속도라고 합니다. 그리고 이에 수직 방향의 벡터 성분, 다시말해 천구면에 접한 벡터성분은 접선속도입니다. 이 두개의 벡터 합이 공간속도가 됩니다.
이 때 고유운동이라는 중요한 개념이 등장합니다. 고유운동은 천구상에서 별의 접선속도 방향의 운동에 의해 나타나는 천구상의 움직임으로, 초각으로 나타내며, 단위는 ''/년(''/year)로 씁니다.
이제 이 개념들을 하나씩 각개격파 해 보겠습니다.
2. 시선속도
관찰자가 바라보는 방향의 속도성분입니다. 천구면에 수직한 방향의 속도이기에 공간상의 위치변화를 알 수 없어, 단순한 안시 관측으로는 알 수 없습니다. 이 때 스펙트럼 분석을 사용하는데요, 별에서는 흡수선 스펙트럼이 나타납니다(이에 관한 내용은 후에 서술하겠습니다.).이 흡수선이 생기는 위치가, 길어지면 적색편이, 짧아지면 청색편이라고 이야기 합니다. 흡수선의 도플러 이동은 아래 포스팅을 참고해 주세요.
지구과학에서 매우 중요한 도플러 효과에 대한 이해
오늘 다루어 볼 내용은 도플러 효과라고 불리는 자연현상입니다. 인터넷 뒤져보면 도플러 효과 정말 많이 찾아볼 수 있습니다만, 앞으로 써 나가게 될 포스팅을 위해 저도 숟가락 하나 얹어볼까
kalchi09.tistory.com
어쨌든, 예를들어 움직이지 않는 별의 스펙트럼이 500nm에서 형성된다고 가정합시다. 그런데 이 선이 490nm에서 관측 되었다면, 원래보다 파장이 짧아진 것이고, 이를 청색편이라고 부릅니다. 이 경우 별은 관찰자에게 접근할 때 나타납니다. 반대로 500nm의 선이 510nm에서 관측되었다면, 이는 적색편이라고 부릅니다. 이 상황은 별이 관찰자로부터 멀어질 때 나타납니다.
시선속도를 계산하는 방법은 간단합니다.

여기서 vr이 시선속도, c는 광속, 람다0은 원래 파장, 델타 람다는 파장 변화량입니다. 이를 이용하면 별의 시선속도를 계산해 낼 수 있습니다.
3. 접선속도
별의 공간운동에 의해 천구상에 투영되어 나타나는 움직임입니다. 시선속도가 육안으로는 관측하기 어려운 것에 비해, 접선속도는 천구에 투영된 실제 별의 이동이기 때문에, 1년 이상의 긴 관측으로 움직임을 찾아낼 수 있습니다. 아까전에도 서술한 것 처럼, 접선속도는 뮤라는 고유운동과 함께 나타냅니다. 다만 정확한 고유운동을 알기 위해서는 별 까지의 거리 d를 반드시 알아야 합니다. 만약 이 거리를 모른다면 무슨 수를 써도 접선속도를 알 방법이 없습니다.
별의 거리 d를 알고 있다면, 1년동안 별이 움직인 각도 뮤와 호도법을 이용해 이동한 실제 거리를 계산하여 어렵지 않게 계산할 수 있습니다.

위의 천구 그림에서 일부만 때 왔습니다. 고유운동은 1년간 별이 이동한 각도이고, d는 별의 거리니까 호도법을 쓰면 됩니다. 그러니까 저 부채꼴에서 별이 이동한 거리 s를 계산하면,

가 됩니다. 속도는 거리/시간입니다. 그런데 고유운동 뮤는 어차피 1년동안 움직인 각도가 됩니다. 따라서 거리 곱하기 뮤 자체가 바로 접선속도가 되어 버립니다. 따라서

가 됩니다. 보통 별의 거리로 많이 사용하는 단위는 파섹(pc)이고, 속도의 단위는 km/s를 사용합니다. 오른쪽 항의 고유운동인 뮤의 단위는 ''/year입니다. 오른쪽 항의 파섹(pc)을 km로 바꾸고, ''/year에서 초각('')은 라디안으로, year는 초(sec)로 단위를 바꿔 줍시다. 그러면
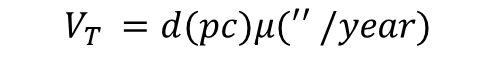
에서 먼저 pc을 km로
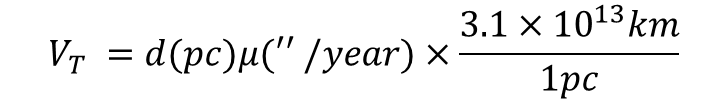
이제 다음으로 ''을 라디안으로
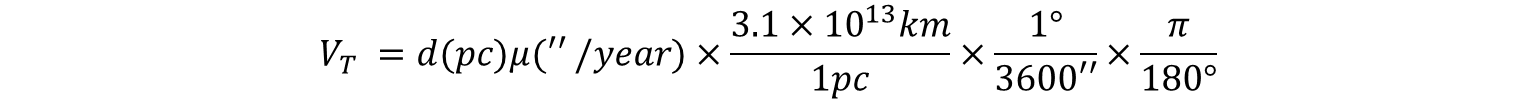
이제 마지막으로 1년을 초 단위로 바꾸면
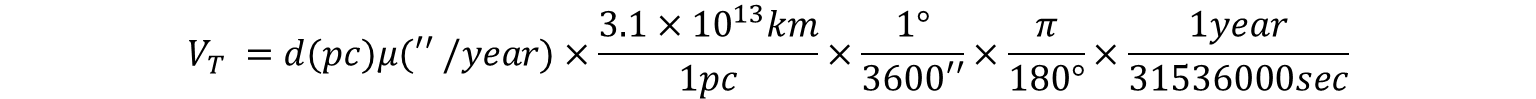
이제 이것들을 모두 계산하면
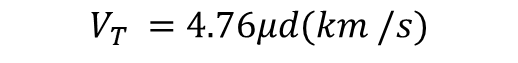
1pc을 km로 바꿀 때 좀 더 정확한 값을 쓰고, 유효숫자를 잘 맞추면
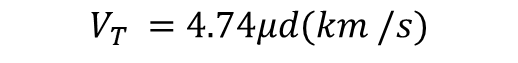
이제 ''/year 단위로 관측한 고유운동값의 단위를 바꾸지 말고 관측한 그대로 뮤에 집어 넣고, 알고 있는 별의 거리를 pc 단위로 저 식에 집어 넣은 뒤 4.74를 곱하면 자동으로 km/s 단위의 접선속도가 튀어나오게 됩니다.
위 계산과정이 엄청 복잡해 보이지만, 하나씩 뜯어놓고 보면 하나도 어려운것이 없습니다. 그냥 단순히 단위를 바꿔주는 과정일 뿐입니다.
4. 공간속도
시선속도와 접선속도의 벡터 합이 바로 공간속도입니다. 시선속도에서 구한 속도와 접선속도에서 구한 속도를 피타고라스 정리를 이용하면 간단하게 공간속도를 계산해 낼 수 있습니다. 그럼 위에 그린 그림에서 이 벡터 그림만 띠어서 보면
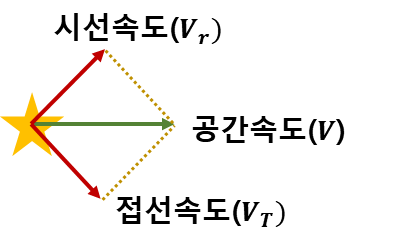
위 그림과 같이 생각할 수 있고, 시선속도와 접선속도의 벡터합이 공간속도가 되기 때문에 공간속도는
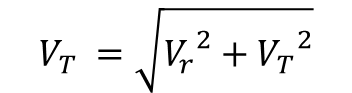
위 관계와 같이 정리할 수 있습니다.
5. 마치며
시선속도와 접선속도, 공간속도의 개념은 별의 운동을 해석하는 것 뿐 아니라 성단의 거리 계산, 태양계 주변 별의 운동 등을 해석하는데 있어서 굉장히 중요한 내용입니다. 앞으로 이에 대한 글을 써 나갈 예정인데, 이를 위해 미리 포스팅을 준비하였습니다.
'교과서 밖 지구과학 > 천문' 카테고리의 다른 글
| 지구과학에서 매우 중요한 도플러 효과에 대한 이해 (1) | 2022.07.23 |
|---|---|
| 지구과학을 위한 원과 타원의 기본적인 내용 (0) | 2022.07.19 |
| 태양계의 떠돌이 별 혜성 (0) | 2022.06.13 |
| 신비한 오로라 현상 (0) | 2022.06.03 |
| 지구 자기장과 밴 앨런 벨트 (0) | 2022.05.31 |




댓글