
지난 포스팅에서 타원 방정식을 이용해 위도별 지구 반지름을 계산해 보았습니다.
그리고 가만히 생각해 보니, 행성들도 모두 타원, 별이나 행성들의 공전궤도면도 거의 대부분 타원 입니다.
그래서 타원 방정식을 그릴 수 있다면 생각보다 많은 것들에 적용할 수 있겠구나 싶어, 여기서는 타원 방정식을 이용해 타원 그래프를 그리는 방법에 대해 알아보고자 합니다.
타원의 정의, 유도, 초점 등의 기본적인 내용은 이번 글의 핵심이 아니니 후에 다룰 포스팅에서 서술하고, 여기서는 타원 방정식을 그래프로 그리는 방법에 집중해 보고자 합니다.
그동안 제가 타원이나 원 방정식을 그릴 때에는 삼각함수를 이용하는 방법을 주로 사용하였습니다. 식을 세우기가 훨씬 간편하고 직관적이었기 때문인데요. 이번에는 고등학생들이 수학시간에 많이 다루는 방정식을 이용해 보겠습니다.
1. 타원 방정식 다루기
타원 방정식은 아래와 같은 관계에 있습니다.

파이썬에서 저 아이의 그래프를 그릴려면, y에 대해 식을 정리해야 합니다. 그럼 y값은 당연히 2개가 나옵니다. 제곱이니까 +와 - 모두 가능하기 때문인데요. 따라서 아래와 같이 정리할 수 있습니다.

결국 그래프를 2개 그려야 합니다. +에 대한 식을 사용하던, -에 대한 식을 사용하던 어느 하나만 그리면 무조건 반원만 그려집니다.
2. 코드 구현하기
타원 방정식이라고 했지만, 결국은 그냥 그래프를 그리는 것이기 때문에, 필수로 사용될 라이브러리는 matplotlib와 숫자를 집어넣을 때 필요한 numpy 이 두가지를 사용할 것입니다. 우선 전체코드를 보시면
import matplotlib.pyplot as plt
import numpy as np
a=15
b=10
c=(a**2-b**2)**0.5
x=np.linspace(-a,a,100)
y1=(b**2-(b**2/a**2)*x**2)**0.5
y2=-(b**2-(b**2/a**2)*x**2)**0.5
plt.figure(figsize=(6,6))
plt.hlines(0,-a,+a,color='black',linestyle='--')##(y축 위치, x축 시작점, x축 끝점)
plt.vlines(0,-b,+b,color='black',linestyle='--')##(x축 위치, y축 시작점, y축 끝점)
plt.grid(linestyle='-.')
plt.scatter(-c,0,c='r')
plt.scatter(c,0,c='r')
plt.scatter(0,0,c='b')
plt.text(-c-2.5,-2,'('+str(round(-c,1))+', 0)')
plt.text(c-1.5,-2,'('+str(round(c,1))+', 0)')
plt.text(-a,a-1,'e='+str(round(c/a,2)),size=13)
plt.plot(x,y1,c='k')
plt.plot(x,y2,c='k')
plt.xlim(-a-1,a+1)
plt.ylim(-a-1,a+1)
plt.savefig("C:\\111\\ellipse.jpg",dpi=300)
plt.show()코드가 길어 보이지만, 어려운 것은 하나도 없습니다.
그동안 소개하지 않은 몇 가지 코드에 대해서만 간단하게 말씀을 드리면
가. 파이썬에서의 제곱 표현
파이썬에서 제곱, 세제곱 등은 * 표시를 2개 붙여서 나타냅니다. 예를들어
- 제곱 : **2
- 세제곱 : **3
- 때문에, 루트 표현은 : **(1/2) 또는 **0.5
가 되겠죠?
나. 그래프에서 수평선 또는 수직선 그리기
수평, 수직선은 아래의 코드를 이용합니다.
plt.hlines는 수평선을 표현하는 것으로, 그 다음 괄호 안의 옵션은 수평선이 그려질 y축값의 위치, 수평선의 시작점, 수평선의 끝점입니다. 예를들어 plt.hlines(0,-10,+10)이라고 쓰면, 수평선의 y축 위치는 0, 시작지점은 -10, 끝 지점은 +10이 됩니다. 위 코드에서 plt.hlines(0,-a,a)라고 한 이유는 간단합니다. 수평선이 그려질 y축 위치는 0이 되어야 하고, 시작점은 -a, 다시말해 -15, 끝 지점은 +15로 장반경을 나타내기 위함입니다. plt.vlines도 마찬가지 논리로 해석하시면 됩니다.
다. 초점을 계산하기
초점의 위치를 계산하기 위해 c라는 변수에 초점의 위치를 계산하는 수식을 넣었습니다. 코드 자체는 어렵지 않지만, 타원이라는 모양 특성상 초점이라는 개념은 매우 중요하기 때문에 따로 언급하였습니다.
라. 값의 문자 표현 및 반올림
plt.text(c-1.5,-2,'('+str(round(c,1))+', 0)')
이 코드를 잘 보시면, plt.text 다음으로 그래프에 들어갈 글자를 지정해 주는 코드 '('+str(round(c,1))+', 0)' 이 나옵니다. 계산한 c 값을 글자로 나타내기 위한 것인데, 복잡하게 저리 해 놓았습니다. 이유는 간단합니다. c에서 계산한 데이터가 문자가 아닌 숫자이기 때문입니다. 저렇게 안하고 그냥 '(c,0)'이라고 하면, c에서 계산된 숫자를 표시하지 않고 당연히 그냥 (c,0)이라고 출력 해 버립니다. 우리가 원하는건 c가 계산한 숫자인데요, 그렇다고 '('+c+',0)' 해도 오류가 납니다. 이렇게 하면 파이썬 입장에서는 문자 + 숫자 + 문자가 됩니다. 예를들어 10+5는 당연히 15로 계산하지만 10+바보 이거 계산 되나요? 안됩니다. c에서 계산한 숫자를 파이썬이 이해할 수 있도록 문자로 취급해 줘야 합니다. 그래서 숫자를 문자로 변화시키기 위해 str(c)라고 취한 것입니다.
그 다음은 반올림입니다. 반올림을 하지 않으면, 일부 계산된 c 값에서 소수점 이하 자리가 10자리가 나올수도 있습니다. 표시할 필요가 없습니다. 유효숫자 몇개만 있으면 되니까요. 따라서 c에서 계산한 숫자를 반올림 하기 위해 round(c,1)이라고 해 준 것입니다. round는 반올림 하라는 코드이고, round 다음 나오는 아이들은 반올림할 숫자, 그리고 반올림 하여 소수점 몇 자리 까지 나타낼지 입니다. round(c,1)이라는 것은 c라는 변수의 숫자를 반올림하여 소수점 첫 자리 까지만 표현하라는 소리가 됩니다. 만약 소수점 셋째자리까지 나타내고 싶다면 round(c,3)이라고 하면 되겠죠?
3. 초점, 이심률에 따른 타원의 모양 변화
이심률이 클 수록 타원은 찌그러진 모양이 됩니다. 타원이라는 것의 정의상 이심률의 범위는 0<e<1 이 되어야 합니다. e=0인것은 원, e과 같거나 크면 포물선, 쌍곡선이 됩니다. 그리고 원에 가까울 수록 두 초점은 중앙에 몰리고, 찌그러진 모양이 될 수록 양 옆으로 치우쳐 집니다.
이를 알아보기 위해 아래와 같은 간단한 짤도 만들어 보았습니다. e가 1일 수록 두 초점이 양 사이드로 벌어지고, e가 0에 가까울수록 중앙으로 몰리는것을 쉽게 확인할 수 있죠?

여기까지, 파이썬을 이용하여 타원 방정식의 그래프를 표현해 보았습니다.
참고로 지구 공전궤도의 이심률은 평균적으로 약 0.017입니다. 엄청 작습니다. 궤적은 당연히 거의 원에 가까울 것입니다.
지구의 공전궤도 장반경과 단반경은
장반경 : 1.0000001124AU
단반경 : 0.9998604869AU
이를 적용하여 그래프를 그려보겠습니다.
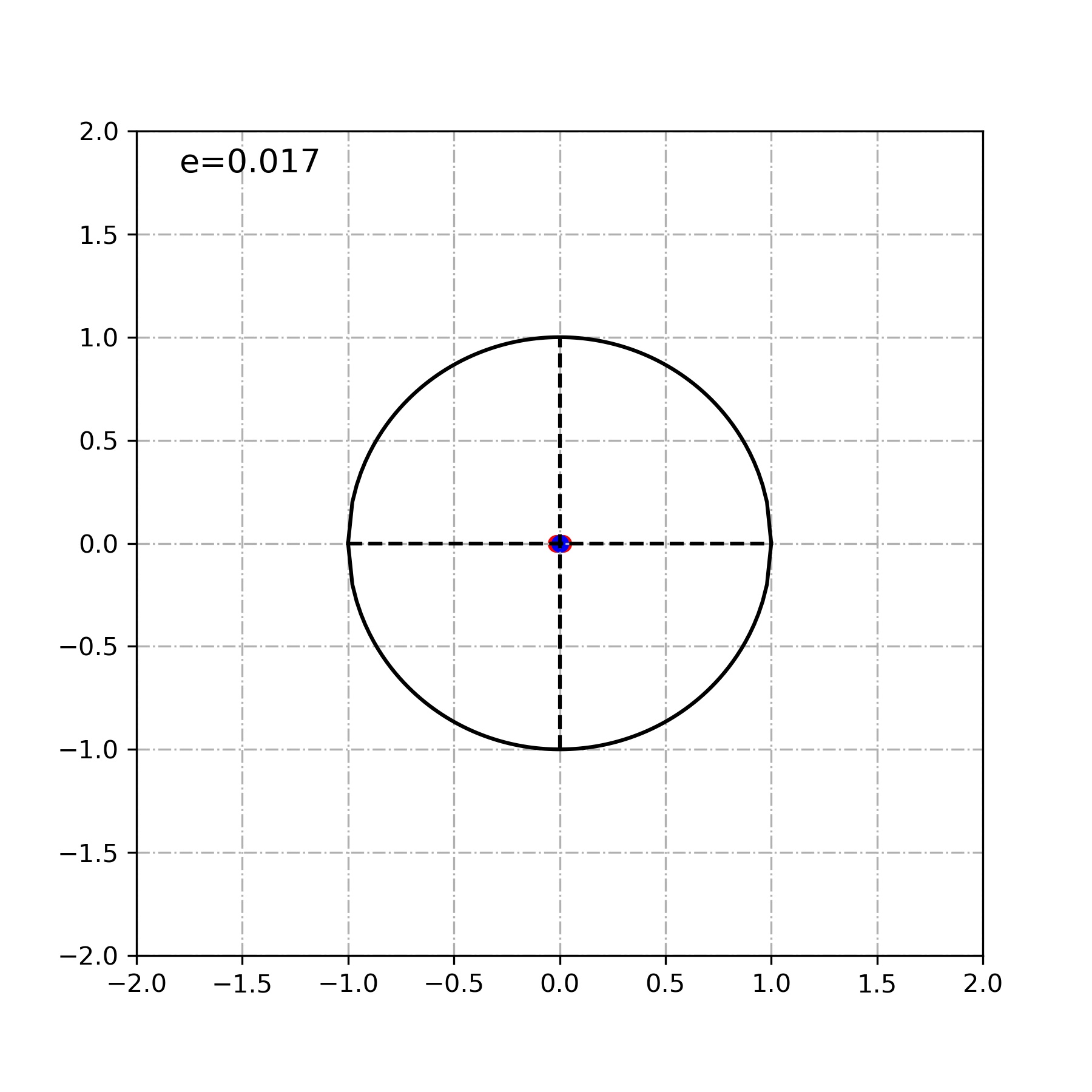
너무도 당연하지만 두 초점이 거의 중앙에 붙어버렸습니다. 이정도면 그냥 거의 원이라고 보아도 무방할 것 같네요.
그나마 이심률이 큰 아이가 명왕성입니다. 대략 0.248 정도 된다고 하네요. 이 아이도 한번 그려보면
- 명왕성 공전궤도 장반경 : 39.48168677AU
- 명왕성 공전궤도 단반경 : 38.24839747AU
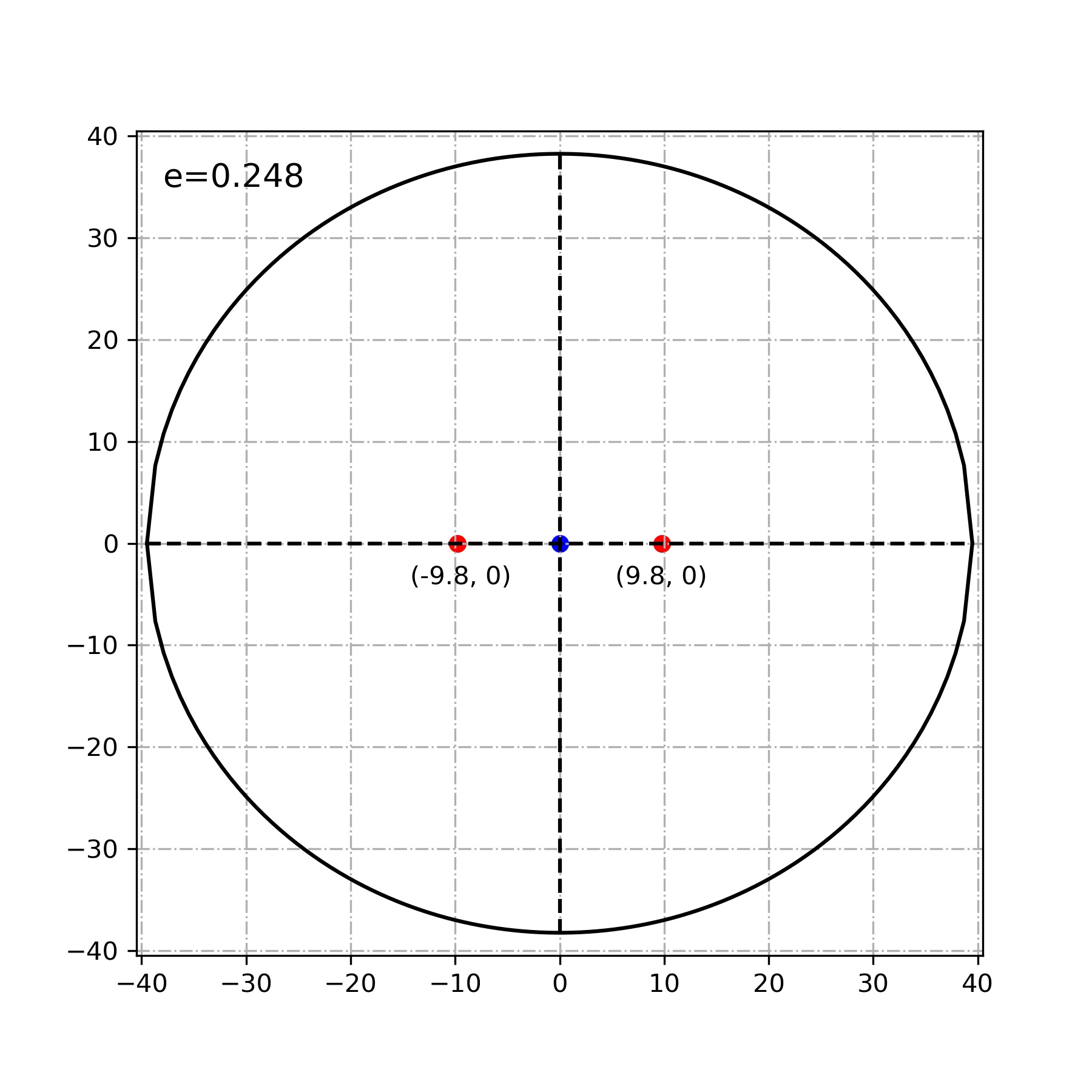
두 초점이 떨어져 있기는 하다만, 그래도 역시 원으로 보입니다.
다음번에는 더 재미있는 파이썬 코드를 구현해 보도록 하겠습니다. 전체 코드를 바로 사용하실 수 있도록 주피터 노트북 기준 파일을 올려두니 필요하신 분은 다운받아 사용하시면 됩니다.
'파이썬으로 배우는 지구과학' 카테고리의 다른 글
| 파이썬을 이용하여 위도별 만유인력, 원심력, 표준중력 변화 그래프 그리기 (0) | 2022.08.24 |
|---|---|
| 파이썬의 막대 그래프를 이용하여 월별 황사 발생 일수 알아보기 (0) | 2022.07.27 |
| 파이썬을 이용하여 위도별 지구 반지름 계산하기 (0) | 2022.06.27 |
| 파이썬을 이용한 바람장미 그리기 두 번째 (0) | 2022.06.17 |
| 파이썬을 이용하여 사진의 RGB 색상 분석하기 (1) | 2022.06.15 |




댓글