
오늘 다루어 볼 내용은 도플러 효과라고 불리는 자연현상입니다. 인터넷 뒤져보면 도플러 효과 정말 많이 찾아볼 수 있습니다만, 앞으로 써 나가게 될 포스팅을 위해 저도 숟가락 하나 얹어볼까 합니다.
1. 정의
어려운 말을 쓰자면 파원이 움직이는 경우 관찰자로 접근 할 때는 파원에서 출발하는 파장이 짧아지고, 관찰자로부터 멀어질 때는 파장이 길어지는 현상을 말합니다.
일상생활에서도 우리는 도플러 효과를 최소한 한 번쯤은 겪어 보았습니다. 다만, 관심이 없어서 그냥 지나쳤을 뿐.
많이들 드는 예가 소방차나 경찰차가 지나갈 때 소리가 달라지는 현상입니다. 아래는 도플러 효과가 잘 나타나는 유튜브 영상입니다. (추후 소방차나 구급차 등이 지나갈 때 제가 촬영해 보도록 하겠습니다.)
아래는 파원이 움직일 때, 그리고 파원은 정지해 있고 관찰자가 움직일 때 도플러 효과를 실험한 사례입니다. 이 역시도 제가 추후 촬영해 보겠습니다.
위의 두 영상을 보시면 이제 도플러 효과에 대해 어느정도 이해하셨으리라 생각합니다.
관찰자가 움직이던, 파원이 움직이던 어찌되었든 둘 중 하나가 움직일 때 관찰자와 파원이 접근할 때는 원래보다 파장이 짧아지고 관찰자와 파원이 멀어질 때는 원래보다 파장이 길어지는 현상이 도플러 현상입니다. 그래서 관찰자와 파원이 멀어지면 소리의 높이(소리의 크기가 아니고 높이입니다. 도레미파솔라시도 같은것)가 낮아지고, 다시말해 중저음이 되버리고, 관찰자와 파원이 가까워지면 소리의 높이가 높아집니다.
아래 그림은 도플러 효과를 설명할 때 엄청나게 많이 쓰이는 그림 중 하나입니다. 영어로 되있지만 쫄거 하나도 없습니다. 그림만 보면 됩니다.

정지한 사이렌의 경우 파장 변화는 전혀 나타나지 않습니다. 하지만 관찰자로 접근하는 사이렌의 경우 가운데 그림처럼 파장이 짧아집니다. 이는 다른말로는 진동수가 증가하는 상황입니다. 그래서 원래보다 고음으로 들립니다. 반대로 사이렌이 관찰자에서 멀어지면 파장이 길어집니다. 다시말해 진동수가 감소하며, 원래보다 저음으로 들리게 됩니다.
2. 천문학 분야에서 나타나는 도플러 효과 1 - 별의 흡수선 변화
지구과학 분야 중 천문학 분야에서 도플러 효과는 밥먹듯이 나타납니다.
별이던 은하던 이런 천체들은 복사에너지를 방출합니다. 복사에너지는 입자이면서 파장의 성질도 가지고 있기 때문에, 이들은 소방차 같은 하나의 파원이 됩니다. 이런 천체들이 지구로부터 멀어지게 되면 위에서 본 것 처럼 파장이 길어지게 되고, 지구에서 가까워지면 파장이 짧아집니다. 물론 문제는 이들 빛은 들을 수 있는게 아니라 볼 수 있는것입니다. 그래서 천체에서 나타나는 도플러 효과는 가시광선일 경우 좀 다르게 관측해야 합니다. 이 때 이용하는것이 천체의 스펙트럼에서 나타나는 흡수선이나 방출선입니다. 흡수선이든 방출선이든 원리는 같으니 흡수선을 기준으로 예를 들겠습니다.
별의 스펙트럼을 관측하면 아래 그림처럼 연속스펙트럼으로 나타나지 않고 중간중간에 검정색 선이 보입니다. 이게 흡수선입니다. 흡수선의 생성 원리는 본 글의 목적에서 벗어나니 이건 나중에 또 포스팅하는것으로 하겠습니다.

많이들 예를 드는 656.3nm 수소선을 사용해 보겠습니다. 중성 수소선은 656.3nm에서 흡수를 보입니다. 그러니까 정상적으로 정지해 있는 별이라면 수소선이 656.3nm에서 나타나야 합니다. 그런데 어떤 별에서 656.5nm에서 흡수선을 보이고 있다고 생각해 보겠습니다. 그 어떤 원소도 656.5nm에서 흡수를 보이지 않습니다. 어? 그럼 이 별에는 우주에 없는 새로운 원소가 있는건가? 라고 생각할 수 있겠지만 그게 아닙니다. 그냥 656.3nm에서 보여야 할 흡수선이 별이 지구에서부터 멀어짐에 따라 656.5nm에서 보인 것입니다. 원래보다 파장이 0.2nm 길어졌습니다. 맞습니다. 이 별은 지구에서부터 멀어지고 있는 것입니다. 파장이 원래보다 길어졌다는 것은 원래보다 빨간 색 방향으로 이동한 것이고, 그래서 이걸 적색 편이라고 부릅니다(아래 그림을 참고하세요).
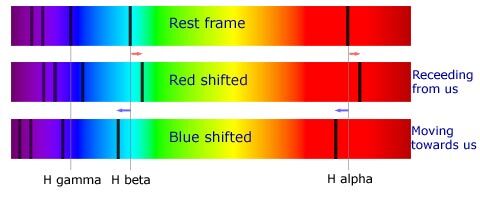
반대 상황을 보겠습니다. 이번에는 656.3nm에서 보여야 할 중성 수소선이 656.0nm에서 관측되었다고 합시다. 이 역시 지구에서는 어떤 원소도 여기서 흡수를 보이지 않습니다. 그렇다면 이 별에 무슨 새로운 원소가 있는게 아니라 656.3nm에서 보여야 할 흡수선이 0.3nm 이동하여 656.0nm에서 나타나는 것입니다. 원래보다 파장이 0.3nm 줄어들었습니다. 이건 별이 지구로 접근하는 상황이 되는 것입니다. 파장이 원래보다 짧아졌다는 것은 원래보다 파란색 방향으로 이동한 것이고, 그래서 이걸 청색 편이라고 부릅니다.
이걸 이용해서 별이 지구로 부터 시선 방향으로 얼마만큼의 속도로 멀어지고 가까워지는지를 계산할 수 있습니다. 이게 시선속도라는 것입니다. 시선 속도는 아래와 같은 간단한 관계로 쉽게 계산할 수 있습니다.
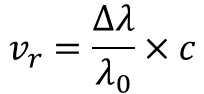
저 식에서 vr이 시선속도, 람다 0은 원래 파장, 델타 람다는 파장 변화량, c는 광속입니다.
만약 델타 람다가 터무니 없이 큰 값을 보여 시선속도가 말도 안되게 크게 나타난다면, 다시말해 광속보다 크다면 이 때는 이걸 쓰지 않습니다. 이 경우에는 상대론적 적색편이라는걸 사용하는데, 본 글의 범위를 벗어나니 여기서는 다루지 않고, 추후에 써 보겠습니다.
천문학에서 도플러 효과는 정말 무진장 많은 분야에서 이용하고 있습니다. 몇 가지를 예를 들면, 위에서 본 별의 시선속도 계산입니다. 이걸 계산하면 태양 근방에 있는 비교적 가까운 별들의 시선속도를 계산할 수 있고, 접선속도를 계산함으로써 공간속도까지 계산해 낼 수 있습니다.
3. 천문학 분야에서 나타나는 도플러 효과 2 - 외계 행성 탐사
외계행성 탐사에도 사용할 수 있습니다. 아래의 짤은 행성을 거느리고 있는 엄청 큰 중심별과 행성이 서로의 공통질량 중심을 돌고 있는 상황입니다. 행성을 거느리고 있는 중심별은 행성과 중심별이 서로간의 공통질량 중심을 돌기 때문에, 지구와의 거리가 주기적으로 멀어지고 가까워 집니다. 따라서 중심별의 스펙트럼에서 미세하게 주기적으로 청색편이와 적색편이가 나타납니다. 이 더럽게 미세한 변화를 감지하여 외계행성을 가지고 있는지 여부를 판단합니다.
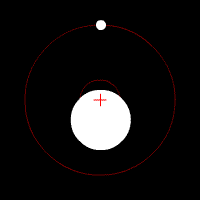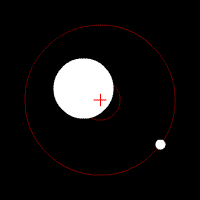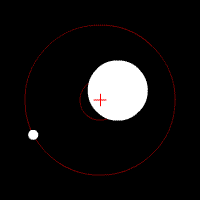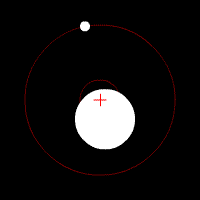
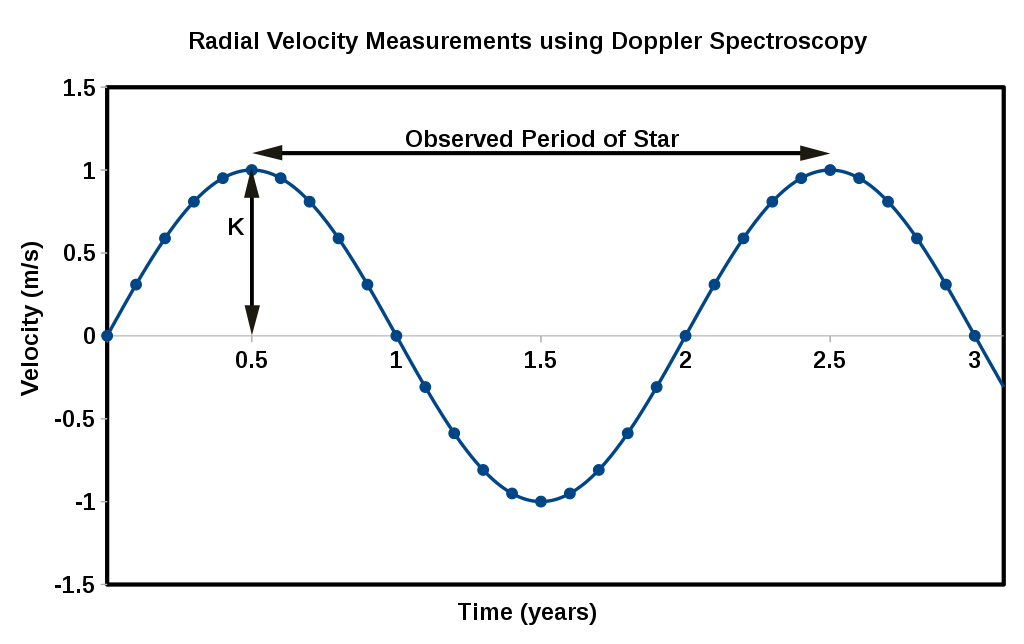
위 그림과 같은 상황에서 중심별의 스펙트럼을 관측하면 아래와 같은 시선속도 변화를 보이게 됩니다.
이거랑 유사하게 쌍성에서도 시선속도 변화가 나타납니다. 원리는 위의 것이랑 완전히 같습니다(아래 그림 참고).

4. 천문학 분야에서 나타나는 도플러 효과 3 - 허블 - 르메트르의 법칙
국부 은하군의 구성 은하가 아니라면, 외부은하들은 모조리 지구로부터 멀어지는 것 처럼 보입니다. 우주 팽창 때문인데, 본 글은 이걸 설명하고자하는게 아니니 이건 나중에 포스팅 하고, 어찌되었든 이것 때문에 외부은하에서 관측되는 스펙트럼에서는 죄다 적색편이가 나타납니다. 허블이 이걸 관측해서 우주 팽창의 근거로 제시했었던건 매우 유명한 사건입니다.
이상으로 도플러 효과에 대한 내용을 마무리 하도록 하겠습니다. 추후에 오늘 다루지 않은 상대론적 도플로 효과에 대한 내용도 한번 다루어 보겠습니다.
'교과서 밖 지구과학 > 천문' 카테고리의 다른 글
| 지구과학 올림피아드 기초강의자료 (0) | 2024.07.14 |
|---|---|
| 별자리로 배우는 천문학 - 오리온 자리 (0) | 2023.04.24 |
| 지구과학을 위한 원과 타원의 기본적인 내용 (0) | 2022.07.19 |
| 별의 시선속도와 접선속도, 그리고 공간속도 (2) | 2022.07.04 |
| 태양계의 떠돌이 별 혜성 (0) | 2022.06.13 |



댓글