
사실 처음부터 위도별 지구 반지름 계산을 생각하고 만들진 않았습니다. 처음에는 위도별 만유인력과 원심력 변화를 그래프로 그려볼 계획이었는데, 가만히 생각해 보니 만유인력은 지구 반지름에 의해 변화하는 값이어서 위도별로 지구 반지름이 어떻게 달라지는지 아는게 우선인 것 같더군요.
그래서 위도별로 지구 반지름이 어떻게 변화하는지 구해보고자 했습니다.
우선 데이터를 찾아보면, 지구 적도 반지름과 극 반지름은 어느곳에나 나와있습니다. 하지만, 예를들어 애매하게 위도 37도에서는 얼마가 되는지는 없습니다. 그래서 아예 계산해 보았습니다.
그리고 단순하게 숫자만 나오면 재미없을것 같아, 지구타원체와 함께 그래프로 그려보았습니다.
1. 필요한 데이터
우선 지구가 완벽한 타원이라고 가정하였습니다. 그래서 적도 반지름은 궤도 장반경이, 극 반지름은 궤도 단반경이 되도록 하였구요. 이에 적도 반지름과 극 반지름은
- 적도 반지름 : 6378.135km
- 극 반지름 : 6356.75km
2. 기본 타원 방정식
타원궤도를 그리기 위해 타원 방정식을 이용해야 합니다. 타원 방정식은 극 좌표계나 일반적인 좌표계, 삼각함수를 이용하는 방법 등이 있는데, 가장 그래프를 잘 표현하는것은 삼각함수를 이용하는 방법이었습니다. 그래서 아래와 같이 삼각함수를 만들어 그래프를 표현하였습니다.

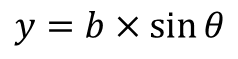
다만, 여기서 그래프를 그릴 때 이대로 두면, 좌표에 음수가 나와 버려서, 음수가 나오지 않게 끔, 실제 코드에서는 아래와 같이 표현하였습니다.

그리고, a와 b에 각각 적도반지름과 극 반지름을 집어넣으면 됩니다.
3. 구현 코드와 실행 결과
이제 기본적으로 알아야 하는 수학 공식은 다 설명하였습니다.
이후 선의 길이를 계산하는 것이 한번 더 나오지만, 이는 어렵지 않으니 패스...
어쨌든 전체 코드를 먼저 보시면
## 라이브러리 호출
import numpy as np
from matplotlib import pyplot as plt
from math import pi
a=6378.135 #장반경
b=6356.75 #단반경
t = np.linspace(0,2*pi,100) ## 0 ~ 2pi까지 100개 숫자 호출
plt.figure(figsize=(7,7))
plt.plot(a+a*np.cos(t),b+b*np.sin(t)) ## 타원 방정식을 이용한 그래프 호출
plt.grid(color='lightgray',linestyle='--')
plt.scatter(a,b) ## 타원 중앙에 점 찍기
plt.hlines(b,0,b*2,color='black',linestyle='--') ## 적도지역 점선 스타일 가로선
plt.vlines(a,0,a*2,color='black',linestyle='--') ## 극지역 점선 스타일 세로선
c=float(input('위도를 입력하세요')) #반지름 알고싶은 위도(?)
posx=a+a*np.cos(2*pi*c/360) ## c 위치의 x값에 점 찍기 위한 수식
posy=b+b*np.sin(2*pi*c/360) ## c 위치의 y값에 점 찍기 위한 수식
linex=[a,posx] ## 타원 중심에서 c까지 선 그리기 위한 리스트 자료
liney=[b,posy]
line=round(((posx-a)**2+(posy-b)**2)**0.5, 1) ## 선의 길이(반지름) 계산
plt.plot(linex,liney) ## 타원 중심에서 c까지 선 그리기
plt.scatter(posx,posy,c='r') ## c 위치에 점 찍기
plt.text(-400,11900,'R='+str(line)+'km',size=12) ## 해당 반지름 값 그래프에 표기
plt.text(-400,12500,'lat.='+str(c)+'deg',size=12) ## 해당 위도 값 그래프에 표기
plt.savefig("C:\\111\\earthrad.jpg")
plt.show()이렇게 하고 코드를 실행하면 아래와 같이 묻습니다.

여기에 반지름을 알고 싶은 위도를 입력하면, 예를들어 우리나라 위도 37도를 입력하면

이렇게 왼쪽 상단에 입력한 위도와 해당 위도에서 지구 반지름이 나오도록 하였습니다.
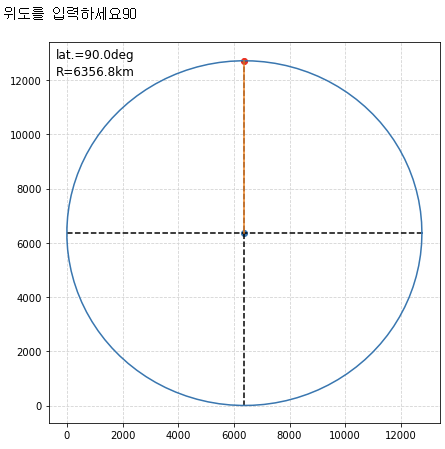
제대로 잘 돌아가는지 극 지역과 적도지역도 샘플로 해 보았습니다. 먼저 극 지역
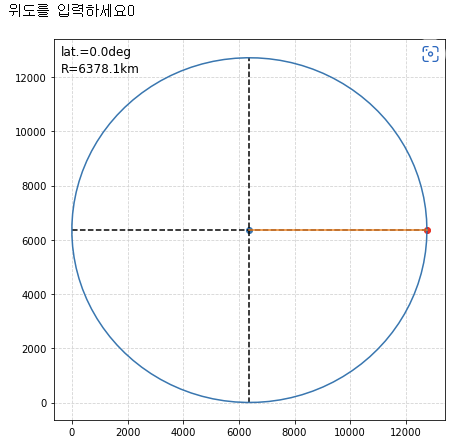
다음으로 적도지역
4. 코드 해석
첫 번 째 세 줄은 단순히 라이브러리를 호출하는 것이니 패스.
a=6378.135 #장반경
b=6356.75 #단반경이 아이들은 장반경을 6378.135, 단반경을 6356.75로 만들어주기 위한 변수 지정입니다. 장반경과 단방경을 다르게 입력하면 다른 행성에도 적용 가능하겠죠? 다른 행성의 편평도 계산에도 활용할 수 있을 것 같습니다.
t = np.linspace(0,2*pi,100)파이썬 관련 포스팅을 하며 처음 linspace라는것을 써 보았습니다. 대학원에 있을 때에는 주구장창 썼던아이인데..ㅎㅎㅎ linspace(a,b,c)라 함은 a와 b 사이 숫자를 c개 토해내라 라는 소리입니다. 예를들어 linspace(0,8,5)이렇게 되 있으면 0부터 10까지 사이 숫자를 같은 간격으로 5개 토해내면 됩니다. 0, 2, 4, 6, 8이 되겠네요. 여기서 중요한건 range와의 차이입니다. range는 for문 없이 단독으로 쓰기 다소 애매한 내장함수입니다. 그래서 range를 사용한 뒤 숫자를 하나씩 출력하려면 for문이 항상 따라다닙니다. 하지만 numpy의 arange나 linspace는 기본적으로 이들 숫자를 일종의 행렬 형식으로 출력하다보니 궂이 for문을 사용하지 않더라도 알아서 모든 데이터를 한번에 계산할 수 있습니다. 0, 2*pi,100은 그러니 결국 0부터 2파이, 다시말해 360도 까지의 숫자를 100개 토해내라 라는 소리입니다.
plt.figure(figsize=(7,7)) 는 쉬우니 패스하고
plt.plot(a+a*np.cos(t),b+b*np.sin(t))
plt.grid(color='lightgray',linestyle='--')
plt.scatter(a,b)a+a*np.cos(t),b+b*np.sin(t)는 수학적 내용이라 다소 그렇긴 하지만, 우선 np.cos이라 하여, t에서 주어진 행렬형 데이터를 마찬가지로 math 라이브러리를 사용하지 않고 np.cos을 사용함으로써 모두 행렬형으로 받을 수 있도록 하였습니다. math라이브러리로 이들 계산을 하면, 아마 오류가 날거에요. 당연한 겁니다. math라이브러리를 사용하면 데이터를 행렬로 처리하지 않기 때문입니다.
어쨌든, a*np.cos(t)라고 하여, 계산하였는데, 만약 x=a*npcos(t), y=a*np.sin(t)로, 삼각 함수에 곱해주는 값이 같으면 이놈은 원이 됩니다. 하지만, x축에는 장반경 a, y축에는 단반경 b를 곱해주면 타원으로 출력이 됩니다. 그리고, 타원의 중심을 0,0에 있지 않고, (6378.135,6356.75)에 두기 위해 각 식에 이 아이들을 더해주었습니다.
plt.grid는 보조선을 그리는 것이고, plt.scatter(a,b)는 타원의 중심에 점을 찍으라는 소리입니다.
c=float(input('위도를 입력하세요')) #반지름 알고싶은 위도(?)
posx=a+a*np.cos(2*pi*c/360)
posy=b+b*np.sin(2*pi*c/360)
linex=[a,posx]
liney=[b,posy]
line=round(((posx-a)**2+(posy-b)**2)**0.5, 1)
plt.plot(linex,liney)이제 중요한 코드는 이아이들이 마지막입니다.
input 함수도 파이썬 관련 포스팅을 하며 처음 다루네요. input하고, 위도를 입력하세요 라고 치면, 위도를 입력하세요 라는 물음과 함께 위도를 칠 수 있는 칸이 나옵니다. 여기에 해당 위도를 입력하면 되는데, 사실 0~360도 모두 입력 가능합니다. 해 보시면 아실거에요..ㅎㅎㅎ
posx와 posy라는 변수를 만들었습니다. 해당 위도에 점이 찍힐 수 있도록 한 함수입니다.
linex와 liney라는 것은 해당 위도에서 반지름을 그리기 위한 리스트 데이터고, 이는 그 아래아래줄의 plt.plot(linex,liney)라는 코드를 통해 그래프로 그려집니다.
line이라는 것은 이 그래프의 길이를 계산하기 위한 변수입니다. 수학시간에 많이들 해 본 공식일 거에요, x축 거리의 제곱과 y축 거리의 제곱을 더한 뒤 2제곱근으로 계산하고, round라는 함수를 이용해 계산결과를 소수점 둘째자리에서 반올림하여 소수점 첫째 자리까지만 표기되도록 하였습니다.
plt.scatter(posx,posy,c='r') ## c점의 위치 표기
plt.text(-400,12200,'R='+str(line)+'km',size=12) ## 계산된 반지름 그래프에 표기
plt.text(-400,12800,'lat.='+str(c)+'deg',size=12) ## 입력한 위도 그래프에 표기
plt.hlines(b,0,b*2,color='black',linestyle='--') ## 적도영역 수평선
plt.vlines(a,0,a*2,color='black',linestyle='--') ## 극 영역 수평선
plt.savefig("C:\\111\\earthrad.jpg") ## 그래프 저장 및 출력
plt.show()나머지 코드는 ##의 주석을 참고하시면 되겠네요.
5. 기타
여기까지 한거 아예 위도에 따라 반지름이 어떻게 변화하는지도 그래프로 그려보았습니다.
즉, 아래 그래프는 위도별 반지름 변화를 나타내는 것입니다.
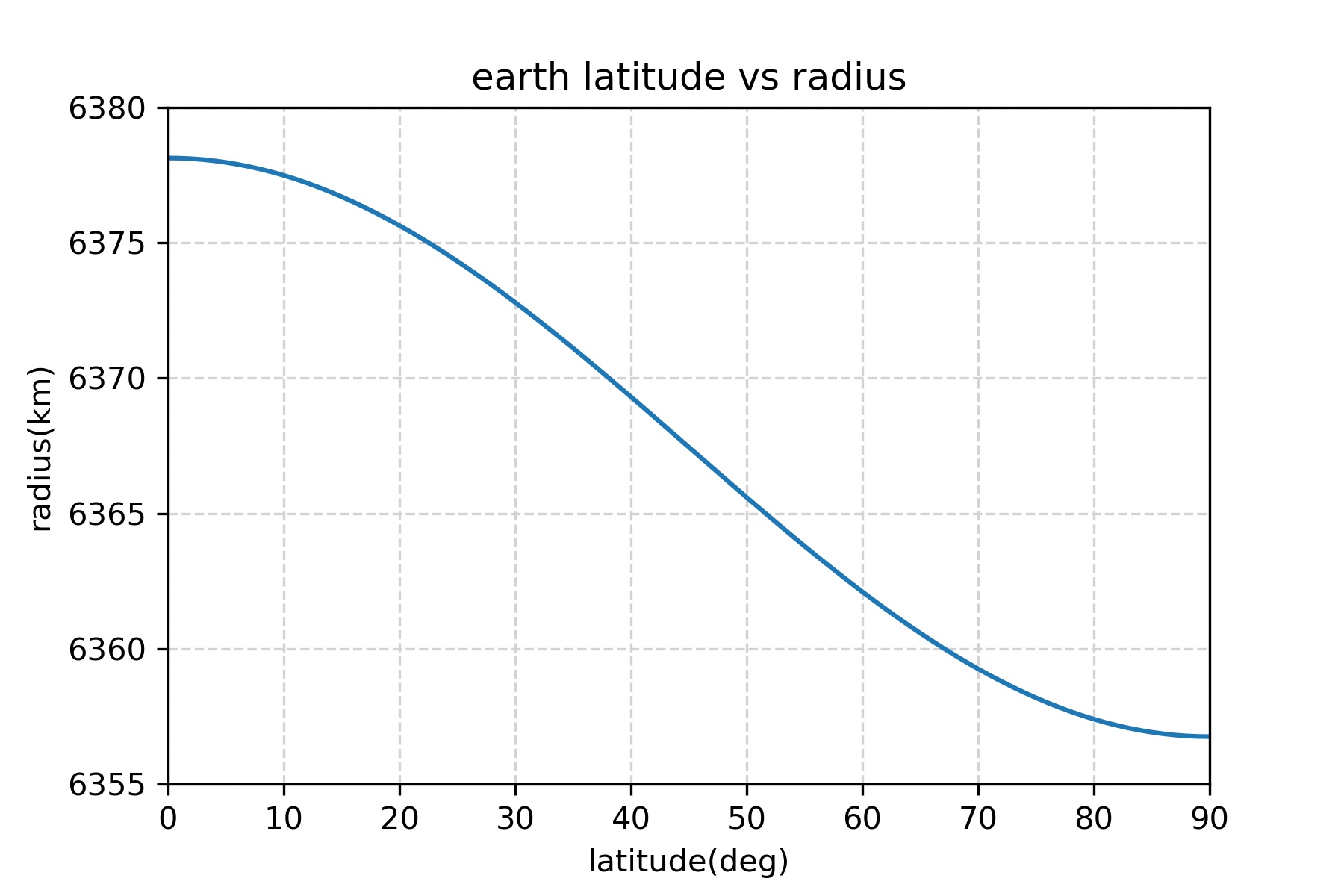
정확한 지구의 위도별 반지름 데이터가 필요하실 분들도 계실것 같아, 위도 10도 간격으로 계산한 결과입니다.

여기까지 긴 글을 마치겠습니다. 다음번 파이썬 관련 포스팅은 더 재미있는 내용으로 찾아 뵙겠습니다. 아래 파일은 주피터노트북으로 돌릴 수 있는 전체 풀 코드입니다.
'파이썬으로 배우는 지구과학' 카테고리의 다른 글
| 파이썬의 막대 그래프를 이용하여 월별 황사 발생 일수 알아보기 (0) | 2022.07.27 |
|---|---|
| 파이썬을 이용하여 타원 방정식 그래프 그리기 (0) | 2022.07.02 |
| 파이썬을 이용한 바람장미 그리기 두 번째 (0) | 2022.06.17 |
| 파이썬을 이용하여 사진의 RGB 색상 분석하기 (1) | 2022.06.15 |
| 파이썬을 이용하여 케플러 제 3법칙을 그래프로 나타내기 (0) | 2022.04.24 |




댓글