
반감기는 지구과학1에서 지층의 절대연령을 측정하는 방법으로 소개되고 있습니다.
문제를 해결하는 과정에서 결과 자체를 해석하는것은 크게 어렵게 느끼지 않는데, 개념이 조금 어렵다 보니 학생들이 다소 힘들어 하는 경우가 많습니다.
오늘은 교과서에서 소개하고 있는 반감기 곡선을 파이썬을 이용해 그려볼까 합니다.
1. 반감기 공식
내용 자체가 수학적 지식이 필요하다 보니 노골적으로 수학이 좀 많이 필요합니다..ㅠ 특히나 그래프를 그려야 하기 때문에 반드시 반감기 공식을 알아야 합니다. 고등학교 지구과학1 수준에서 다루는 모원소와 자원소, 그리고 반감기의 관계는 아래와 같습니다.

여기서
Nt=남아있는 원소(자원소)의 양
N0=처음 모원소의 양
T=반감기
t=걸린 시간
입니다.
이걸 이용하면 몇 가지 간단한 명령어를 통해 반감기 그래프를 그려낼 수 있습니다.
2. 필수 라이브러리
1차원 행렬 배열을 불러올 numpy와 그래프 작성에 필수인 matplotlib가 필요합니다.
import numpy as np
import matplotlib.pyplot as plt이렇게 하면 필수 라이브러리는 모두 불러온 셈입니다.
3. 반감기 공식 이용하여 기초 수식 입력하기
다음으로 초기 모원소의 양, 반감기, 시간 변화량을 불러올 코드를 짜겠습니다. 간단합니다.
T=1.0*(10**8)
No=100
t=np.arange(0,3*(10**11),1000000)
Ntp=No*(1/2)**(t/T)
Ntd=100-No*(1/2)**(t/T)- 변수 T에 반감기를 넣었습니다. 1.0x10^8로 T를 넣어, 반감기가 1억년이라고 가정하였습니다.
- No=100이라고 하였습니다. 초기 함량을 100으로 한 것입니다. 퍼센트 변화를 보기 위해 초기 모원소양을 간단하게 100으로 하였습니다.
- 시간 변화 간격을 np.arange를 사용하여 0부터 10^11까지의 숫자를 1000000, 그러니까 백만 간격으로 출력하게 하였습니다. 이걸 백만이 아니라 1이나 10같은걸로 하면, 파이썬 입장에서는 1부터 1천억까지 모두1 간격으로 계산해야하니 결과를 보는데 시간이 엄청 걸리거나 에러메세지를 띄웁니다. 그래서 저렇게 숫자 간격을 크게 한 것입니다.
- Ntp는 모원소의 변화입니다. 반감기 공식을 그대로 사용하였고, 저렇게 함으로써 모원소가 지수함수적으로 감소하는것을 보게 될 것입니다.
- Ntd는 자원소의 변화입니다. 100에다가 모원소 함량을 빼면 바로 자원소 함량이 나오기 때문에, 간단하게 100을 빼 주었습니다.
여기까지 하셨으면 다 끝났습니다. 이제 간단하게 그래프만 그리면 됩니다.
4. 그래프 그리기
그래프는 학생들이 많이 다루는 모원소와 자원소 함량 2개를 그릴 것입니다.
plt.plot(t,Ntp, label='parent isotope')
plt.plot(t,Ntd, label='daughter product')
plt.legend()
plt.grid()
plt.xlim(0,500000000)
plt.savefig("C:\\111\\radioisotope.jpg", dpi=300)
plt.show()첫 번째 plt.plot에서는 x축을 t(시간)의 변화로, y축을 모원소의 함량 변화로 나타내었고, 범례(레전드)를 주기 위해 label을 사용하였습니다.
두 번째 plt.plot은 자원소의 양 변화를 나타내었고,
plt.legend()를 사용하여 범례를 표시하도록 했습니다.
plt.grid에서는 보조선을 나타내었습니다.
plt.xlim(0,500000000)로 잡았습니다. 저걸 잡지 않으면 불필요하게 x축 범위를 너무 길게 잡습니다. 반드시 잡아주어야 우리가 잘 아는 그래프가 튀어나옵니다.
어쨌든 이렇게 하여 결과는

짠 하고 우리가 잘 알고 있는 결과가 나왔습니다. x축에 1e8이라는건 신경쓰시지 않아도 됩니다. 무슨 의미냐면
1x10^8, 그러니까 각 숫자에 1억을 곱해준 값이라는 뜻입니다. 그럼 1은 1억, 2는 2억....5는 5억이 됩니다.
x축과 y축에 그래프 이름을 넣으면 완성 될 겁니다. 그래프 축 이름을 집어넣는건 어렵지 않으니 여기서는 생략.
여기서는 예제로 반감기가 1억년인 어떤 원소를 가정했고, 그래프가 나온 결과를 보아도 반감기가 정확히 1억년에서 모원소와 자원소의 그래프가 교차하는것을 확인할 수 있습니다.
전체 코드는 아래와 같습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
T=1.0*(10**8)
No=100
t=np.arange(0,3*(10**11),1000000)
Ntp=No*(1/2)**(t/T)
Ntd=100-No*(1/2)**(t/T)
plt.plot(t,Ntp, label='parent isotope')
plt.plot(t,Ntd, label='daughter product')
plt.legend()
plt.grid()
plt.xlim(0,500000000)
plt.savefig("C:\\111\\radioisotope.jpg", dpi=300)
plt.show()5. 그래프의 y축을 로그 형태로 표현해 보기
교과서에서는 다루지 않지만 그래프의 y축을 로그로 표현하면 좀 재미있는 결과가 나옵니다.
이번에는 반감기를 5000년으로 잡고 수를 계산해 보겠습니다. 그러면 아래와 같은 코드를 생각해 볼 수 있습니다.
import math
import numpy as np
import matplotlib.pyplot as plt
T=5000
No=100
t=np.arange(0,30000,1)
Nt=No*(1/2)**(t/T)
plt.plot(t,Nt)
plt.grid()
plt.yscale('log')
plt.xlim(0,30000)
plt.show()위에서 짠 코드와 거의 같습니다. y축을 로그로 표현하기 위해
plt.yscale('log')
를 추가하였고, 반감기에 맞게 np.arange의 일부 숫자만 변경해 주었습니다. 이렇게 놓고 결과를 보면
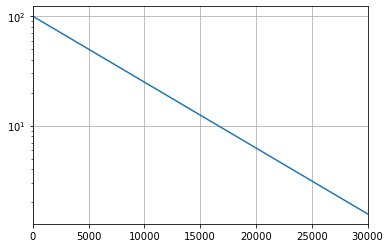
y축을 log로 잡아버리니 예상한 것 처럼 직선, 1차함수같은 그래프가 나왔습니다.
이번에는 계산 범위를 늘려보겠습니다. arange의 숫자를 30000이 아닌 0두개 더 붙여서 3000000으로하고, ylim의 범위도 0두개 더 붙여서 30000000으로 하겠습니다. 나머지는 동일하게
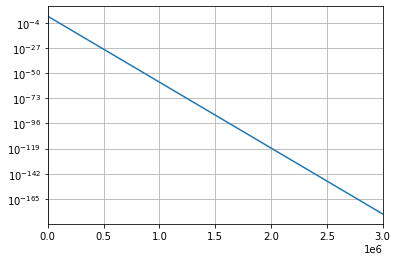
너무도 당연하지만 모원소의 숫자가 10^-185까지 떨어지면서도 절대 0이 나오지는 않습니다. 결국 이론상 모원소는 죽어도 0이되지는 않는다는 소리입니다. 지수함수값이니 이론상 모원소는 때려죽여도 0이 되진 않고, 0에 무한히 수렴한다 생각하시면 됩니다.
여기까지 이번 포스팅을 마치고 다음번에도 쉽고 재미있고 의미있는 파이썬을 가져와 보겠습니다.
'파이썬으로 배우는 지구과학' 카테고리의 다른 글
| 파이썬의 원 그래프(pie chart)를 이용하여 해수에 녹아있는 염분비 표현하기 (2) | 2023.04.16 |
|---|---|
| 파이썬을 이용해 지구과학2에서 다루는 단열선도 그리기 (4) | 2022.10.10 |
| 파이썬을 이용하여 해수 경도-깊이별 컬러맵(color map) 그리기 (2) | 2022.10.04 |
| 파이썬을 이용하여 해수 경도-깊이별 등수심선(contour line) 그리기(feat. scipy 를 이용한 데이터 보간(interpolatio (6) | 2022.10.02 |
| 파이썬을 이용하여 전파 은하 Centaurus A 분석하기 (1) | 2022.09.30 |




댓글